[1] In electrostatic problems, it is sometimes necessary to calculate the total charge on the Dirichlet boundaries. Similarly, in magnetostatic problems, we can calculate the total flux crossing such boundaries. This can be done by integration of the potential obtained by solving the Poisson equation.
First, pardon me for the mathematics that follows. Let us assume we need to solve the total flux flowing in a magnetic circuit. We have the currents given to us. We solve the Poisson equation to find the magnetic potential. Let us call the vector magnetic potential to be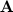 
and the current density vector to be 
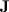. Then we have the traditional
where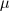 
is the permeability. If the unit vectors in x, y and z directions are
,
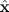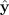and
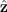respectively, we can rewrite the Poisson equation as
but we only have currents along the z direction, i.e.
. Hence, we end up with the scalar Poisson equation where we have only
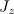non zero and need to solve for
.
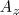After finding 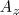, we can find the flux density 
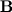by taking the curl, i.e.,
which is equal to
Finally, we can find the total flux
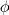by integrating flux density, i.e.
where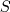 
is the surface area of the Dirichlet boundary. Since we know the triangles on that boundary, we can do this by breaking down to each triangle.
Even though the above discussion is related to a magnetostatic problem, we can apply the same procedure to an electrostatic problem. The only difference will be that instead of calculating the flux, we will be calculating the charge.
The integration can be done by using -> menu option. It will print out the integrated value (charge or flux) on the terminal.