Table of Contents
In this chapter, we will study in detail the input file format and defining a physical problem to be solved by pdnmesh. I must apologise that I use a description and notation heavily biased to electrical engineering problems. But if you know what you are doing, you can adapt any problem to be solvable by pdnMesh.
It should be noted that (currently) only 2 Dimensional plane problems can be solved. Typical physical problems are:
Electrostatics
Magnetostatics
Fluid Flow: Laminar Flow Problems
Heat Flow: Steady Heat Flow
Eigenvalue Problems: Helmholtz Equation
Microwave and Optical Waveguides
The Poisson equation in rectangular coordinates can be written as:
and
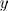are the rectangular coordinates.
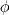is a scalar, generally called the potential.
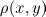is also a scalar, dependent on
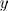and
.
and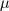 
are dependent on the medium properties. The former is called the permittivity and the latter is called the permeability of the medium. For instance, in Electrostatics,
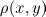would actually mean the (negative) charge density and
will be the permittivity of the medium. In magnetostatics,
is ignored (or made equal to 1) and
is used to characterize the medium. Please note that you do not need the absolute values for
and
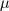. You can use the relative permittivity and relative permeability instead.
The first step should be to convert the PDE to be solved into above form.
The scalar, homogeneous Helmholtz equation, or Wave equation, can be written as:
where
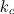is the cutoff frequency. The variable 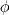can be either the Electric field or the Magnetic field. Once we know the cutoff, we can find the propagation constant, 
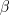using the relation,
This is an eigenvalue problem because
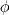appears in the derivative as well as in the stand alone term. The eigenvalues will give us the possible values for
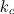or cutoff. The smallest value of cutoff will give us the dominant mode.
This equation is used to solve homogeneous waveguide problems. For non homogeneous waveguide problems, we need to solve the vector Helmholtz equation. However, in all cases obtaining the propagation constant 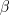using the eigenvalues of the solution 
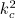is the same.
Note that the Poisson's equation can be considered a special case of the Helmholtz equation. In the next sections, we will see how to prepare a problem suitable for input to pdnMesh.